Lately I investigated new ways of constructing big integer numbers, and came up with the Operator function
bigO in
an essay.
I have new plans for operator matrix bigO2, and cubic and further dimensions bigO to arrive at a Prodigy function that iterates over bigO's dimensions.
All these numbers are integers and in theory still countable, but not in practice.
In fact the apparatus to create these big numbers has become so profound, that only a few enlightened mathematicians beside myself will be able to understand it ;o)
I hope to come back later to describe the new formulas to create ever larger numbers.
For now there's the
essay.
Of course the majority of these awfully big integers will remain beyond description. That happens for example already with many integers somewhere..
..inbetween 3^^3 and 4^^4, while
3^^3 = 3^(3^3) = 7,625,597,484,987 and
4^^4 = 4^(4^(4^4)) ~ 1E(8E153)
Numbers in the vicinity of 3^^3 (about eight trillion you'd say) are well expressible in the decimal number system, but not if your system was counting on fingers: 111...
In fact counting an average three fingers per second, counting 3^^3 would take you 806 centuries.
Many of the numbers in that vicinity have never been seen before by any human being (though 7625597484987 itself has become quite familiar to you now ;o)
So if there is a horizon, beyond which more and more integers start to become inexpressible, this depends on the system you use to express them in.
This is our luck, for now we can study the concept of a number horizon from different perspectives.
What perspectives besides counting on fingers and the decimal number system do we have?
And what are the advantages of each number system in expanding our integer horizon a bit further?
We'll explore two 'worldly limits' to cardinality of the set of numbers:
The binary system uses 2 as its number base or radix.
Each extra digit takes you an extra exponent of 2 further, any number inbetween can be expressed, no number is left behind, as in any number system with a radix.
On a computer with an extraordinarily large hard disk running Microsoft's
NTFS
file system,
you currently have a maximum file size of 16 terabytes minus 64 KB. This determines your physical horizon for expressing numbers:
With 8 bits per
byte,
you have 8*(2^44-2^16) = 140737487831040 bits at your disposal.
This means you can positively store any number up to 2^140737487831040-1.
If you'd think of printing your data, the base 10 exponent is 140737487831040*log(2)/log(10) which tells you that most such numbers require 42366205351537 decimal digits.
Which means you have to run 118 record
Océ printers
for one year to print out such a number in decimals, consuming 21183 metric tons of paper, almost as much as the
annual consumption of paper by a small city like
Delft.
Let's be reasonable, such behaviour would be unnatural. The hunters for Pi know one practical use for storing billions of digits -beside the thrill- and that's for testing computer systems. You can let a new system calculate a certain number of digits of Pi and compare the end digits of the result with the known end digits, to check if there's an error. Many stored digits of Pi have never been looked at by a human being.
A number horizon is a practical concept, not so scientific, rather philosophical. A mathematician might pass by and say, "Hey, let me push your horizon a bit further". We don't mind, we know many numbers are easily expressible and many more must be physically inexpressible. And that there is some blurry horizon inbetween.
For example: I regularly use my fingers to illustrate small lists I make in my mind, mostly just counting to five. On our fingers we can count to ten, with fingers and toes we can come to twenty. Twenty is a practical limit for finger counting purposes. Inbetween ten and twenty things can get a little messy, missing a toe or two as you bend over and fall.
After twenty any reasonable person would use an
abacus
or write a number on a clay tablet or on a piece of paper.
The abacus imposes some kind of ordering on your beads, for example in groups of five, and then you have rows of beads that count numbers of beads.
I imagine with ten rows on such a base 6 abacus you can count to 6^10-1 = 60466175.
Perhaps you can add another abacus, but then things can become messy, as your customers lose track of what you are doing.
It's time to learn how to write numbers!
With the digit values 0,1,2,3,4,5,6,7,8,9 in decimal base we can express every number we physically need.
We could write down the number of particles at present in the universe in about 80 decimals, if we could determine it exactly.
The notation that you use in any radix to write your numbers is this:
an*10^n + ... + a2*10^2 + a1*10^1 + a0*10^0
Example: 2*10^3 + 0*10^2 + 0*10^1 + 7*10^0 = 2007
After which you get the option of writing a dot (comma in other European languages) and appending an optional decimal fraction (mostly this fraction will be an approximation).
Then the decimal number system is nothing more than two virtual abacuses, with in theory an unlimited number of rows, and nine possible beads on each row.
Here we concern ourselves with integer numbers that do not have a decimal fraction, so we can use just one such virtual abacus.
Using our radix 10 number system we can pinpoint where fingers and real abacuses cease to function. So much so, that from our perspective it is hard to see that one day in the past these numbers lay beyond the horizon of the human being using these primitive tools.
You already witnessed how I wrote down the number 4^^4, that was definitely NOT expressible in the decimal number system and also not in ANY radix based number system.
For if you had as many characters at your disposal as there are code points in the standard
UNICODE set, that is all the digit values needed in a radix 65536 number system, then you'd still need far too many digits.
Radix Digits formula: ifa^b = r^d , then d = b*log(a)/log(r)
Example:4^(4^(4^4))in base65536takes4^256*log(4)/log(65536) ~ 1.7E153digits.
Self-substitution (ofd in r) in the Radix Digits formula converges to the numberr^^2 = r^r
and to the sobering fact that: radix~5.32E151expresses4^^4in~5.32E151digits.
Radix based number systems just cannot express such a large number fully, mathematics can: 4^^4.
But then there's still the issue of representing all the numbers in the vicinity of 4^^4 that lay beyond our radix number system horizon.
How can we keep track of these mathematically? Are there alternative number systems?
I'd like to believe there's a natural horizon for the expression of decimal numbers at:
10^10 = 10,000,000,000.
Also the maximum number of people our planet can cope with, a limit for humanity.
Numbers beyond ten billion are rarely written in full, as individuals. A scientist would rather use exponential notation: 10^10 = 1E10.
Following the same belief, the natural horizon for hexadecimals,
numbers notated in radix 16, would lie at 16^16 = 18,446,744,073,709,551,616 ~ 1.8E19.
Maybe the maximum number of intelligent beings a galaxy can harbour before it overstretches its resources... I recommend using this radix in your Milky Way too ;o)
r^^2
by clicking it in last weblog.
For a computer your number input is a String,
that is: a variable size array of character values each typically a byte long.
To be able to do arithmetic this String must be parsed into an internal bit representation of the number.
This representation can be thought of as an array of fixed size in which the entries are either 0 or 1.
The JavaScript
in your browser performs its calculations faithful to the 64-bit
floating-point standard,
which expresses a number in double size, as shown in the picture.
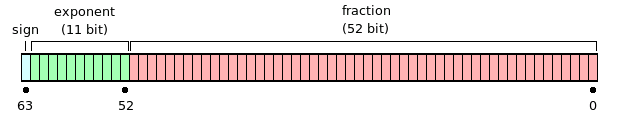
The largest double number inside the machine is about 1E308.
The largest integer (says Flanagan's JavaScript)
is 2^53 = 9007199254740992 ~ 9E15 ~ 13.9^^2.
That largest exact integer is the number horizon of the browser,
our current standard horizon to rely on.
We can express a number in any radix 2 or larger, knowing that representation is the only one possible for that number. Each number is uniquely represented. This seems obvious, but there are some radices, those inbetween 0.5 and 2, where each number has an infinite amount of representations.
For example in radice 1, you can write the number 3 as
111 or 10101 or 101.0001.
More curiosity:
radice 1 is the only positive radix that cannot represent fractional numbers.
The JavaScript Array is well suited to study new number systems,
as it has a variable length, it can contain numbers and Arrays
as well as other types,
and Arrays can be nested to variable depth.
To be able to cover currently inexpressible numbers, such as 4^^4,
you'd need a number system where digit values themselves are composite.
An Array's nest depth could correspond to the levels of operators used: + * ^ ^^ ... that operate on the Array's number entries.
We might reserve every index 0 for meta information about the Array, such as the depth at which it nests other Arrays.
Such a new number system should make it easy for us to perform at least two levels of operator functions on its numbers, in the same way the decimal system allows for easy human addition and multiplication. Scaling back and forth between levels of operators is the very property that makes numbers practical in use.
Because we have little experience beyond our radix perspective, let's study an alternative, combinatorial system to do arithmetic, more suited for large numbers:
The
Factoradic number system,
based on the factorial numbers:
k! = 1, 2, 6, 24, 120, 720, 5040, ... where
1*1! + 2*2! + 3*3! + ... + k*k! = (k+1)! - 1
Where the maximal digit value is increasing at the same pace as the digits length,
and the 'radix power' increases as the factorial of the digits length.
This system uniquely represents every number.
Factoradic numbers are not quite up to the task of expressing 4^^4,
this still takes at least 5.32E151 factorial digits
(as the limit of
((k+1)^(k+1)-(k+1)!*(k+1))/(k^k-k!*k)/k ~ 2.72 ~ e), but it's a start!
This weekend I realized that the number system I thought could help us
write down all big numbers
in a simpler way by using expanded operators ^^..., cannot exist.
If it did exist, it would supply almost unlimited
data compression
without loss of
information,
it would be the greatest invention of all time.
Pity it's proven to be mathematically impossible, to write the universe on a floppy disk
(a floppy disk that contains itself :o) Nevertheless, ponder its uses:
The human genome has some 3E9
base pairs.
Each base pair can be of 4 types, so that a
sample
in this sequence looks like: ATAAACCTGC. Mathematically the genome is a number in
radix 4, each digit taking 2 bits, so our sample could be represented as the number 0300011321 and stored in bits as 00110000000101111001.
To store the information that each human cell stores in its
24 chromosomes
you need about 6E9 bits: 750 MegaByte on a harddisk.
To store the 'whole' human genome as it is, of
all people,
without compression, you'd need to reserve 4E19 bits:
4.4 Exabyte,
which is close to the estimate of current monthly
internet traffic in the world.
You can binary store the exact number 2^1E20 as a 1 followed by 1E20 zeros, but that would be foolish. There is little extra information in those zeros, meaningful internet traffic never looks like that.
Same with 10^1E10, which may seem a random series of bits, but cannot contain a lot of extra information, because its quite easily expressible in another number system. When a number lacks information, the internet traffic would never look like that.
Even the different binary packages that make up a number like 9^(9^9) could never hold a binary representation of a computer program, because a series of programs always contain a lot of information, and the original number 9^^3 doesn't, because it is reducable
(in my bigO system)
to just 2 bytes.
On the other hand, many numbers inbetween
8^^3 = 6Mb and 9^^3 ~ 146Mb
(Mb calculated by: log(a)/log(2)*a^a/8/2^20)
are well suited to represent an advanced browser program like
SeaMonkey.
It can be taken for granted the SeaMonkey number is maximally random and unreachable by simple operations, and that it has its own mathematical vicinity (its own directory in which it stores preferences, urls, images and plugins) which is just as unreachable by simplifying mathematical notation as the original SeaMonkey number itself, because in essence this vicinity of numbers is what SeaMonkey can be.
It is possible to set up an operating system so that it adds a certain number to a mathematically compressed (encrypted) form of SeaMonkey, but the number you add will have to be nearly as random as SeaMonkey and require just as many bits. For practical purposes it would be the same as knowing SeaMonkey beforehand.
I was wondering whether an operating system like Windows might by pure chance translate a mathematically formulated number to a meaningful program? And if so, if the chance that it translates another formulated number to another meaningful program is much, much smaller or zero? Of course the formulated numbers themselves hold no information, but the operating system does, as it is a random number. The new program might not be explicitely defined, but under the surface then it is. I guess such an operating system could be called wasteful.
This only makes sense if the axiom of the impossibility of lossless compression of unspecified data is true. From this axiom follows that the mathematical vicinity of many large numbers (those numbers surrounding it that are reached by simple mathematical operations and functions thereof) are unsuitable to contain much information. As the number of operations that determine such a vicinity grows, so does the amount of information that can be stored by the numbers thus reached.
This means there are two types of numbers: random numbers (expressed binary) that can store information, and mathematically formulated numbers that are hopeless as information sinks. And that there's a point where these two types of numbers merge, where a formulated number becomes able to contain information.
There's a horizon for numbers, that is defined by the number and order of mathematical operations: by the information you need to create numbers.
Each number has an
information entropy,
and its entropy depends more on the number's position than on its size, but position is determined by the basic operators allowed in the number's mathematical universe.
Things cannot fully describe themselves, therefore a universe in which things can describe something fully, must be random universes in which things are created by randomness. For if a universe was a law, a mathematically formulated number without (ever more) random digits, and the scientist inside it could describe the law that describes the universe fully, the scientist would have described the scientist fully and the number the description is would contain itself.
Evolving means adding randomness. Mathematics as it evolves is becoming a random universe.
Yet without order all is chaos. Mathematical laws and numbers are needed to interpret random data. The horizon inbetween may be the number space that is most interesting.
Tools for such an inquiry can be handed by the expanded operators ^,^^,... A number system based on expanded operators, though not ubiquitous over the natural numbers or perhaps not as reducing as the binary system, may still be of great use.
My speculation is that either the rate of randomness in the physical universe is larger than any operator expansion can describe, or that the operator functions cannot be reduced further, so that ^^ is fundamentally incapable of explaining something about or being reduced to the exponential numbers created by ^.
As ^^^ has the same relation to ^^, as ^^
has to ^ (but not as ^ has to *),
you need only to look into the relation ^ and ^^ of adjacent operators. Of course a higher level, one that counts over the operators, may supply other insights.
In yesterday's
weblog
I made a mistake, I said, "no formulated number can store much information".
If I was to correct it there, I'd have to rework the total argumentation, which was quite wonderful, except for that suspicious error on which my conclusions were based. I must apologize, for I am new at information theory, and hand you my explanation now:
If you employ multiple systems of describing data, you must proclaim which system you use in the beginning. It's wise to use the superb binary representation for default, and to specify the first bit as holding the information for a choice between "binary | formulated" numbers. In this system of choice for all numbers up to a certain maximum, the first "switching bit" is already INFORMATION.
Now, all the axiom of non-compression (the impossibility of lossless compression of unspecified data) can tell you is that this system of choice cannot be better than the binary system on its own. No matter if you have just one alternative algorithm or can pick from a great many (eg. 2^63) algorithms to formulate your numbers, no matter how many/few or how large/small the variables can be that you feed those algorithms.
The binary system is in total (over a range starting at 0 up to the last possible number) as least as good.
That is what the axiom of non-compression means. And yesterday's conjecture that numbers are either random or formulated, and that a number's randomness is information entropy, and that there's an interesting horizon between random and clear numbers, does not follow. Because the one switching bit tells you that, if some numbers may be compressed in an alternative formulation, the majority of numbers aren't. Because sometimes a large randomly generated number looks non-random purely by chance.
For example: a program may by chance be expressible in a number like 9^^3, which can save 146Mb storage space if you write it as the formulated number [00001001,0011,11], but the chance that such an event happens is so remote that it doesn't pay to reserve the {1,15} bits of memory space to be able to use this [8,4,2] bits formula for compression.
Let's set up an experiment to test the axiom of non-compression:
Suppose we take the number that stores all information for a
SeaMonkey browser,
which I am told is 33403504 byte long,
in the order of 2^33403507 ~ 1E10055458,
and we store that number in the BigInteger SEAMONKEY.
And we devise a number system of choice with a simple 8-bit formula
containing just the byte p,
which must be read as:
BigInteger decompressedProgram = SEAMONKEY + p
We tell everybody the SEAMONKEY number, so they can use this decompression.
The decompression program itself would then be slightly larger than a SeaMonkey browser.
With this program we can at least decompress SeaMonkey, if we put p = [00000000].
And so we gain SEAMONKEY-9 bits by decompressing a lovely browser.
For each other number that cannot be decompressed, the cost is just 1 bit for my switch.
The total cost depends on the range of numbers covered,
here we use the range up to SEAMONKEY*2^8+255
for the purpose of testing the axiom of non-compression - that end number seems a lot bigger, but it's only 1 byte longer than SEAMONKEY.
So the cost would be SEAMONKEY*2^8+255 extra bits,
if no other number is decompressible using our system of choice.
Then "cost minus gain" would result in an average decompression COST of:
(SEAMONKEY*(2^8-1)+246)/(SEAMONKEY*2^8+256) ~ 1-2^-8 ~ 0.996 extra bit.
Not so inefficient...
But suppose the SeaMonkey program allows a bitmap of 8 preferences to be appended at the end of its bit range, and that the initial preferences aren't set.
Then decompressing with the other values our variable p can take,
namely 1 to 255, will result in a browser with added functionality.
The total gains could then be counted for 256 browser states in 257*(SEAMONKEY-9) bits,
because for SeaMonkey no preferences means the same as a preferences bitmap of 0.
The total costs would be: SEAMONKEY*2^8-1 bits.
And "cost minus gain" results in an average decompression GAIN:
(SEAMONKEY*(2^8-257)+2312)/(SEAMONKEY*2^8+256) ~
(2312-SEAMONKEY)/(SEAMONKEY*2^8+256) ~ 2^-8 ~ -0.0039 extra bits.
Such decompression pays off just a little, which must be an error.
Even more so, if the preferences bitmap of SeaMonkey (or any additional 'bitmap images'), would be sufficiently large we would reserve more bits for the variable p. These extra bits could also be used for compressing other programs, where we'd first subtract the SEAMONKEY number and then store them in p.
Is the axiom of non-compression refuted by this experiment? What's wrong?
Solution to yesterday's
problem:
You'd have to have at least one bit set inside the
SeaMonkey program,
to flag whether it had a preferences bitmap coming. That makes SeaMonkey a bit longer and "cost minus gain" the case result in a decompression LOSS, in support of the axiom of non-compression.
My system was "double edged", I was using the bit length of a number as an additional source of information (telling if a bitmap comes appended). In our example, as [0] is not physically the same as [], with the first bit in p
I sent 1+2 = 3 numbers.
Sometimes you can slightly increase the information load by adding a little 'good old counting', but you still can't beat the binary system, which has a longer array of bits n, physically capable of storing 2^n+n "double edged" numbers (that name was suggested to me by
marco,
who also came up with the term "'triple edged'" numbers, where I guess each digit value is a
variable size
Array
of numbers).
If SeaMonkey always expects a preferences bitmap of 8 bits appended, the "cost minus gain" is:
SEAMONKEY*2^8 - 256*(SEAMONKEY-9) = 256*9 bits.
This is a greater cost than when we would declare our preferences bitmap to be part of the browser program: with a new number
SEAMONKEY_PLUS = SEAMONKEY*2^8+255 and a "cost minus gain" of only:
9 bits.
But then our decompression program would have to be 8 bits longer.
As for decompressing data by adding the SEAMONKEY number to a larger variable
q = [000000000...] to create a totally different program,
that program would have to be of almost equal size to make the gain worthwhile.
long q = PROGRAM - SEAMONKEY // compress BigInteger decompressedProgram = SEAMONKEY + q // decompress
Because q>p>=0 and NUMBER_MAX = SEAMONKEY+2^QBITS-1, the gains for decompressing a SeaMonkey browser are smaller than before. The losses for numbers higher than SEAMONKEY+p that cannot be decompressed, become much greater.
To acquire enough small gains to compensate for its original costs, our new compression tool would have to compress a lot of programs that start with the same system declarations in the highest bits, and that are of exactly the same bit size as SeaMonkey. Then, because we're able to subtract the value of the highest exponents, we would lose a few bits. This does add up, and we would have developed a primitive decompression tool for SeaMonkey-like programs.
However, the axiom of non-compression tells us that over all the numbers from 0 up to
NUMBER_MAX there can never be any gain of any compressor over the binary system.
We expect more of a certain type of data, taking programming peculiarities into account, so our numbers aren't strictly random anymore. But can this overrule the axiom of non-compression, which is the impossibility of lossless compression of unspecified data?
As I'm fed up now with all this SeaMonkey business, instead of making more calculations,
we'll go to the bigO
Opera :O)
The binary system is really something special. Most people would think of a large number as the sum of a large series of terms where radix powers are multiplied by digit values. Multiplication iterates over addition, and powers iterate over multiplication. (People won't admit that they do this, but it's how the number system in radix 10 works, people are decimal automatons!)
[dcba] = d*10^3 + c*10^2 + b*10^1 + a*10^0 x+y = O(x,y) x*n = O(x,n,1) = O(x,O(x,...,O(x,x))) #x = n x^n = O(x,n,2) = O(x,O(x,...,O(x,x,1),1),1) #x = n
You can indeed write down the numbers in radix 2 like that, but actually the binary numbers can be composed from addition in another way, without any need for multiplication or exponents, summing only the recursions of the function:
B(i) = B(i-1) + B(i-1) B(0) = 1 B(1) = 1 + 1 = 2 B(2) = (1+1) + (1+1) = 4 B(n) = O(O(...O(1,1),...), O(...O(1,1),...)) = 2^n
If you'd create your binary numbers by summing the different values of the Operator-like function B, you just leave out the exponents you don't need, no zero and no multiplication is involved. This looks very efficient, but how to note down such a series?
It's easier to write a 0 if you skipped a place,
then to have to write down each place you're at.
And without a radix system you'd have to go back to basics, just 1 way to mark your place:
with your finger 111...
But if you're in a fluid state without linear order, and you have to throw all your binary digit values n in a pool, B(n) will be your system. For you can also notate each place using the system B itself, provided you can neatly wrap up the atomic 1's in transparent layers.
For example: elf = 1(1)(1(1)), whose atoms can be ordered in eleven other ways
(watch the nesting).
The binary system can't be beaten, it can't be improved, because you can't compress binary information to smaller binary information.
Same goes for the "finger counting" system, it can't be beaten if you cannot have an array of digit values, because you cannot stick out more fingers than you're sticking out.
What you CAN do with a binary array of values, is create a system of choice that compresses certain very large numbers significantly better. For example, here's a system for positive numbers, that uses 32 bits and expresses half its values as regular integers and the other half as binary exponents.
The 1st bit is the switch and the following 31 bits are used like so:
- if the 1st bit is 0, the next bits represent a number n
in the range n = [0, 2^31-1] = [0, 2147483647]
- else the next bits represent a number m = 2^(31+n), where the binary exponent is in the range [31, 2^31+30]
This 32-bit system can represent every number up to 2,147,483,678 and from there on many larger numbers up to a maximal decimal exponent of 1.89E646,457,002,
much larger than JavaScript's Number.MAX_VALUE = 1.79E308.
But there is no resolution of numbers inbetween, like you have with the usual approximation by a
mantissa, the mantissa here is always 1.
You can reserve m bits for that,
then the highest expressible number will be 2^m*(2^(31-m)+30).
I think my 32-bit system is a useful alternative for storing large positive numbers. But it skips a whole lot of numbers inbetween, and that's why it cannot touch the axiom of non-compression.
Finally, it does make clear why the binary system cannot be the host of a better number system that covers all numbers up to a higher maximum. It's as simple as "counting fingers", there just aren't more choices c to create 2^c numbers than the number of bits in a binary series. Quite self-evident after all...
Huzza! I found my system for expressing large numbers. It's yesterday's nested notation for the binary
system B,
that offers the required variable arrays of numbers to help us travel further than before.
Each 1 at nest depth n represents a power 2^^n, that grows faster than exponentiation.
B can be biologically implemented and permits negative scales in a three valued logic. In a cell B the number soup is constantly adding (and subtracting) atoms 1, of which the digit molecules take care themselves, ain't it wonderful? More about system B below the picture.
Let's go over the theory of the natural limits for creating large numbers, the number horizon, once more:
Not every number down from a certain large enough size is expressible in a perfect system with limited resources. As soon as numbers grow bigger many escape the representation dance of any natural system.
The binary system does best in managing the resources of binary bits, I investigated this in the past five weblogs. When you have m memory bits at your disposal, if you want enough space to express ALL numbers below 2^m, your memory is full. For your next memory array the binary system is again best, and then you can express ALL numbers below (2^m)*(2^m). Etcetera.
To write down 4^^4 = 4^(4^(4^4)) = 2^(2^513) ~ 1E(8.07E153) in a natural binary or exponential system cannot be done,
unless the exponent may be expressed exponentially (as you see). You can reserve standard bits for such double exponents or make it part of a system of double choice using a nested switch bit.
Holes will inevitably fall inbetween, where inexpressible numbers are hiding,
only to creep out when you invent new ways to get them out (like some new nested bigO(a,b,c) recursion).
But your formulas can never be inventive enough to get all large numbers out, because your number of inventions is limited, as your systems consist at best of unique choices, formulated by small binary mathematical programs, that are limited in size.
The total S of the choices a system can make, infers that if your system is a number system (bound), it is itself minimally expressible by the number 2^S-1, and it does not cover a greater range of exact numbers than the information in a binary system with S bits, in principle [0,2^S-1], or perhaps [0,2^S+S].
In principle, if any number system can define 2^S,
it isn't perfect over the numbers: there's at least 1 inexpressible number smaller than its own size. A formula system with
free variables
is bound to leave holes later too, for when a free variable can be any number up to T, the upper limit of the choice bits it has is log(T)/log(2), unless of course you straight away jump to infinity.
In reality, because people are busy, formula systems grow, have a certain fuzzy natural maximal size, but do not define it. Such systems also leave holes small and large: many big numbers that cannot be expressed if the system had to cover their complete range. Theoretically we wonder how fast a minimal mathematical system must grow to fill the holes it leaves behind by the numbers it cannot express that are smaller than its own size - now that's an iteration!
Anyhow, some numbers below and the majority beyond your system's size escape the dance of formulation.
You can allow randomly formulated numbers, eg. created by a streetwise formula that you add to your system, which specifies a
range:
"X is a positive integer below 2^N".
Then you can express the
probability
0<=P(X)<=1
that a number in a certain bitwise range is expressible within the number system of which the random formula is part.
All well known numbers have P(X)=1, but above some unknown number horizon the chances of finding expression drop steadily.
I define a random formula as a mathematical
function
applied within the context of a number system,
but also with a free variable, that is restricted to a certain
domain, but not applied to one specific case x=n.
If you keep options open you can still say something about the function's range and the probability a number can be created given a semi-random domain. What a random formula must do, is make a prediction about randomly set bits in a certain range. When a bit value is otherwise unknown it tells for example the chance the bit is set is P(X)=1/2, or overall that it is P(X)=2^-N.
That's basically chance: a toggle between 0 and 1, an unknown bit.
Later on you'll run into trouble again: some bits below N cannot be located anymore, because some of the exponent numbers N are vanishing behind the horizon. The chance of toggling these bits within a certain part of the domain diminishes. You can then try to redefine the probability a range of numbers finds expression within your system as a nested toggle: (1/2)^M, or overall (2^-N)^M, small and insecure...
Because such probabilities cannot be exactly settled in the upper ranges of large systems, there should have been a lot of insecurity in the first place, but as less and less numbers inbetween are mathematically formulable, we come to know less and less about the chance these number ranges (of number ranges of ...) find expression.
But perhaps I'm going to fast here, perhaps the probability of number ranges within a semi-random number system could be an elegant instrument to describe the state of affairs over the
first number horizon.
And it makes me wonder, if quantum-level uncertainties are ruling the physical waves, how big must the number of the mathematical super-structure be? And is our physical universe to be trusted, isn't it a renegade sub-system that trives on inflating the ultimate, stealing away more space for its own mischievous sub-schemes? This big black tear our universe is, with its stars and galaxies so far apart, it could easily be a melodrama staged in the number hell of Hollywood, to seduce you and me to do evil maths :o(
The 17th century scientist
James Bernoulli
took as his motto
"number variations reoccur". If the same number follows from different calculations, it can be used to improve formulas to describe otherwise random data. Without systematic explanation repeating results are not so beautiful, for they take up the space of other numbers, which will be lost
"below the horizon" of your inapt sub-system.
The elegance and simple roots of mathematics should be enough to prove it's innocence. And it's not without honour to help the real world get their system right :o)

I'm a proud daddy, you must see the baby pictures!
My table shows the numbers 0 to 16 in the ^^ nested binary biological number system
B notation:
| decimal | binary | bit B | bio B |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 10 | (1) |
| 3 | 11 | 101 | (1)1 |
| 4 | 100 | 100 | ((1)) |
| 5 | 101 | 1001 | ((1))1 |
| 6 | 110 | 100010 | ((1))(1) |
| 7 | 111 | 1000101 | ((1))(1)1 |
| 8 | 1000 | 1010 | ((1)1) |
| 9 | 1001 | 10101 | ((1)1)1 |
| 10 | 1010 | 1010010 | ((1)1)(1) |
| 11 | 1011 | 10100101 | ((1)1)(1)1 |
| 12 | 1100 | 101000100 | ((1)1)((1)) |
| 13 | 1101 | 1010001001 | ((1)1)((1))1 |
| 14 | 1110 | 101000100010 | ((1)1)((1))(1) |
| 15 | 1111 | 1010001000101 | ((1)1)((1))(1)1 |
| 16 | 10000 | 1000 | (((1))) |
| ... | ... | ... | ... |
| 65536 | 10000000000000000 | 10000 | ((((1)))) |
Level 5 brackets might follow at 2^^5 = 2^65536 ~ 1E19728
In bio B
all atoms can float freely within their bracketed space, as no order can be imposed in a fluid medium, but the sum within the enclosure stays the same.
The column bit B
gives a bit system notation for bio B,
where brackets are written as zeros, and start brackets are left redundant.
There are no two number 1-atoms next to each other,
as these would merge to a number 2-atom.
You will never see two the same atoms close to each other.
In the biological soup these number atoms meet all the time, and form a
wrapper with one atom inside, or may
attach a label with a nesting value to one atom, which I propose are
(either way or combined) chemical mechanisms to form higher number values (such as 2).
Likewise other, more complex mergers take place to add numbers.
Some numbers are not so economical, such as the exact number
15 or the gargantuan 65535.
These numbers need never be formed, as chemically more reducing mergers take prevalence, and there's an abundance of number molecules floating in the soup to add up, without wasting too many atoms and labels, and without compromising the result of the addition, as in nature an approximate number is always good enough.
The free floating atoms could be the working memory of the cell, while the more deeply nested numbers are better suited to hold the more permanently encoded long memory contents. Such persistence effects could better be achieved by keeping two (or more) different chemical calculators.
A 3-logic system where negative 1-atom molecules can be added inside the brackets to either form exponential values between 1 and zero, or to erase a positive 1-atom, can be more precise and sends more resources back into the cellular medium.
Adding number values inside the 1st layer is the same as multiplication, adding numbers on the 2nd level works like exponentiation.
The wrapped or labeled atoms should chemically be able to complete all atomic number additions without help. When numbers have to be obtained from the wrappers, a reading mechanism might squeeze the wrappers to complete all mergers, and chemically read off the information the wrappers contain during the process.
If number system B is employed by the living cell, the number thus extracted will have to be transported via axon potentials and
neurotransmitters
to other living cells.
Man is a beast of addition and multiplication, it's hard for him to imagine what comes after, what comes before and what's inbetween his two most familiar recursive operators.
| operators | examples |
|---|---|
|
0 = N(x) = x' N(-') = 0 |
N(0) = ' = 1 N(1) = '' = 2 N(n-1) = '''... = n |
| O(...) = O(...,0) |
O() = O(0) = 0 O(x) = O(x,0) = x |
|
O(x,n) = N(N(..N(x).)) = x + n O(x,-n) = -O(-x,n) = x - n |
0(2,3) = ''''' = 5 0(0,0) = 0 + 0 = 0 0(1,-1) = 1-1 = -0 |
|
O(x,n,1) = O(x,O(x,....O(x,x).)) = x * n O(x,n,-1) = O(x,O(n,-1,2),1) = x/n |
2*3 = 2+2+2 = 6 1000/10 = 100 |
|
O(x,n,2) = O(x,....O(x,x,1)...,1) = x ^ n O(x,n,-2) = log(x)/log(n) |
2^3 = 2*2*2 = 8 log(100)/log(10) = 2 |
|
O(x,n,3) = O(x,....O(x,x,2)...,2) = x ^^ n |
2^^3 = 2^(2^2) = 16 n^^-1 = 0 |
|
O(x,n,4) = O(x,....O(x,x,3)...,3) = x ^^^ n |
2^^^3 = 2^^(2^^2) = 65536 n^^^-1 = 0 n^^^-2 = -1 |
|
O(x,n,p+1) = O(x,....O(x,x,p)...,p) = x ^^^... n |
O(2,2,p) = 4 O(2,3,p) = O(2,O(2,3,p-1),p-2) O(x,0,p) = 1 {p>0} O(x,1,p) = x {p>0} |
|
B(0) = 1 B(i) = O(B(i-1),B(i-1)) B(n) = O(2,n,2) = O(n,n,3/2) |
B(3) = 2^3 = 8 B(4) = 2^3 + 2^3 = 2^4 = 16 B(-1) = 1/2 B(1/2) = 2^(1/2) |
|
B(n,1) = B(B(..B(1).)) = O(2,n,3) |
B(1,1) = B(1) = 2 B(4,1) = B(B(B(B(1)))) = 2^(2^(2^2)) = 2^^4 = 65536 |
To approximate the number that fits the universe you
take as unit the smallest possible length, the
Planck length of
L = 1.616252E-35 meter,
of which there are
L^-3 = 2.3685E104
in a cubic meter of space, and
9460730472580800*L^-3 = 2.2408E120
in a cubic light year.
Multiply that by the current
size of the universe,
which is a
sphere with a volume of
4/3*pi*(156E9/2)^3 = 2E33
cubic light-years,
then you get the current total of
5E153
Planck volume units in the universe.
Then there's the fourth dimension, which has a
Planck time
of
T = 5.391214E-44
second, or
1/T*60*60*24*365 = 5.85E50
Planck time units per year.
Multiply that by the current
age of the universe
and by its volume, and take roughly a quarter, then you have
5.85E50*13.7E9*5E153/4 = 1E214
possible Planck space-time events up to the present.
The hidden 7
curled up dimensions of String theory are according to a generous estimate at most
0.15 millimeter big, in total
(1.5E-3/L)^7 = 1E224
extra hidden Planck units.
The current string space with 11 dimensions would then spit out a universal number of at most
1E214*1E224 = 1E438 Planck units.
If every Planck unit needs to be represented separately as 0 or 1, or if indeed every Planck unit means a choice, a binary probability, instead of a fixed state, then up to the present the universe has received a number of choices in the range
4^^4 < 1E1E438 < 5^^4.
You can speculate about the end of space-time, but there are most likely no interesting phenomena to occur when the universe has reached its
final state,
that is if all matter has collapsed into neutron stars and black holes.
According to the maximum estimate that final collapse is reached 10^10^76 years from now, if the universe is still there...
In the end the total number, as the universe keeps expanding in 11 dimensions,
is maximally
1E438*(10^(10^76-51))^11 = (1E1E76)^11 = 1E1E836
Planck units big.
(If your universe was part of a
multiverse
with less than
1E1E835 universes with similar laws,
the total of Planck-like units would still be about
1E1E836)
In
holographic
theories of the universe every choice is not binary, but creates a whole new universe itself. Then the final number of the holographic universe would be in the range
4^^5 < 1E1E1E836 < 5^^5.
This proves that our universe is not very big compared to the countable numbers we can create with the first three operators of the bigO function O(a,b,c).
Systems rule above numbers, a system number horizon is typically an operator level bigger than the number horizon for a free variable, as a system contains these numbers as choices. Else the holes inbetween the variable level numbers will get too big or remain too small, and the system level cannot relate the variable level numbers anymore, as was hinted at in last weblog.
Our universe or physical multiverse, because it appears physically as a bunch of free variables bound by laws, must be a sub-system of a bigger system
ruled by a God if you will, a
Brahma heaven.
Then that Brahma heaven system, to still have some grip on the lower level physical universe,
can be represented by a number that is only an operator higher than ours.
About O(4,4,4) = 4^^^4 will do,
but not exactly...
God's number,
as it represents His super-system, will have such an amount of apparent randomness that no mathematical formula or number system in this universe can express it exactly.
I call my estimate
O(4,4,4)
the Alpha-4-Mann number, because it is related to the
Ackermann numbers.
The best estimate of the Number of God is hereby given.
These days I will repeatedly break the record
for the largest exact countable number ever expressed on Earth.
(I leave it to you to add 1, so you can be the next record holder :o)
We'll continue where we stopped counting in last weblog's
bigO table,
after the definition of the first three terms of the bigO operator function.
In the new table below, we'll study the Alpha-Mann numbers, together with a whole
alphabet
of Mann numbers,
to define the next terms of bigO, so its list of terms becomes countable.
At that point we own a more practical and improved version of the bigO operator function,
which I introduced so flamboyantly in my essay
One Last Thing.
After this we can systematically expand bigO
by turning its parameter list into a multi-dimensional matrix,
defined by Lady numbers iterating over the previous array of terms.
In the construction of bigO in the table below each parameter keeps a certain part in creating the whole number, whereas in other constructions the final term dwarfs the earlier terms and dominates the result.
Follow me closely now.
| formula | examples |
|---|---|
|
O(a0,a1,a2) =
[term a0 iters #a1] O(a0,...,O(a0,a0,a2-1),...,a2-1) = [^ iters #a2-1] a0^^^...a1 |
O(4,4,2) = 4^4 = 4*4*4*4 = 256 O(4,4,3) = 4^^4 = 4^(4^256) O(4,4,4) = 4^^^4 = 4^^4^^4^^4 = O(4,O(4,O(4,4,3),3),3) |
|
Alpha-a-Mann numbers: 0M1a = Ma = O(a,a,a) |
M0 = O(0,0,0) = 0 + 0 = 0 M1 = O(1,1,1) = 1 * 1 = 1 M2 = O(2,2,2) = 2 ^ 2 = 4 M3 = O(3,3,3) = 3^^3 = 7625597484987 |
|
Bravo-a-Mann, Charlie-a-Mann, and next Mann numbers: M2a = O(Ma, Ma, Ma) M3a = O(M2a, M2a, M2a) Mb+1a = O(Mba, Mba, Mba) |
Bravo-2-Mann: M22
= O(4,4,4) = Alpha-4-Mann: M14 cMb0 = 0 cMb1 = 1 |
|
O(a0,a1,a2,b) = O(Mba0, Mba1, Mba2) |
O(2,2,2,1) = O(M2,M2,M2) = O(4,4,4) O(2,1,1,2) = O(M22,1,1) = O(4,4,4) |
|
1-Alpha-a-Mann, and next c-Mann numbers: 1M1a = O(a,a,a,a) cM1a = O(a,a,a,...,a) with c+3 equal terms a else if b>1 cMba = O(m,m,m,...,m) with c+3 terms m = cMb-1a |
1M12 = O(2,2,2,2)
= O(M22,
M22,
M22) 2M12 = O(2,2,2,2,2) 1M22 = O(1M12, 1M12, 1M12, 1M12) 2M22 = O(2M12, 2M12, 2M12, 2M12, 2M12) |
|
O(a0,a1,a2,...,ac+2, b) = O(cMba0, cMba1, cMba2,..., cMbac+2) |
O(2,2,2,2,2) = O(1M22, 1M22, 1M22, 1M22) O(5,4,3,2,1,0) = O(1M15, 1M14, 1M13, 1M12) |
| O(..:, 0) = O(..:) | O(a,0,0,0,b) = 1Mba |
The algorithm in today's second table is extremely fast.
We enter the multi-dimensional phase of the Lady numbers, which we name by
animal alphabet system:
Zebra, Ant, Bear, Cat, Dog, Elephant, Fox,
G...,
and create from the triple Mann numbers from above,
redefining the first dimension of bigO and expanding subsequent rows.
The fat red record numbers are beyond explanation.
| formula | examples |
|---|---|
|
Ant-t-Lady numbers: 0L1t = Lt = O(a,...,a) with tMtt terms a = tMtt |
L0 = 0 L1 = 1 Ant-2-Lady: L2 Ant-27102007-Lady: L27102007 |
|
O(a0,...,am; b0,...,bn) = O(a,...,a; Lb0,...,Lbn-1,bn-1) with Lt terms a = Lt where t = O(La0,...,Lam; Lb0,...,Lbn-1,bn-1) |
O(1,1; 1) = (L2-3)-Alpha-L2-Mann: L2-3M1L2 O(2,7,1,0; 2,0,0,7) |
|
Bear-t-Lady, and next Lady numbers: L2t = O(a,...,a; a,...,a) 2 rows of L1t terms a = L1t Lrt = O(a,...,a; ..: ; a,...,a) r rows of Lr-1t terms a = Lr-1t |
DogZebraFox-2007-Lady: L27102007 |
|
O(a0,0,...a0,k; ..: ar-1,0,...ar-1,m; ar,0,...ar,n) = O(a,...a; ..: a,...a; Lrar,0,...Lrar,n-1,ar,n-1) where rows < r have Lrt terms a = Lrt where t = O(Lra0,0,...Lra0,k; ..: Lrar-1,0,...Lrar-1,m; Lrar,0,...Lrar,n-1,ar,n-1) |
O(1,2,3,4; 5,6,7; 8,9; 10) BearIbisLionWhaleZebraKangaroo -28102007-Lady: 0L2810200728102007 |
|
1-Ant-t-Lady, and next 1-Lady numbers: 1L1t = O2(a,...a; ..: a,...a) 0L1t rows of 0L1t terms a = 0L1t 1Lrt = O3(a,...a; .:: a,...a) cubic r squares with side 1Lr-1t and equal terms a = 1Lr-1t |
1-Ant-28102007-Lady: 1L28102007 |
|
O3(a0,0,...a0,k;
..: ar,0,...ar,m;; 1) = O2(a,...a; ..: a,...a) is a square with side 1L1t and terms a = 1L1t where t = O2(1L1a0,0,...1L1a0,k; ..: 1L1ar,0,...1L1ar,m) |
O(30; 10; 2007; 1) |
An outline for further Record Generation:
Thus bigO is made to accept a parameter of multiple dimensions. A second parameter, also of multiple dimensions, can be added, with the function of expanding the dimensions, sizes and entry terms of the first. Then a third multiple dimension parameter expanding the previous two parameter dimension blocks, etc., until bigO's multiple dimension parameter list has itself become of multiple dimensions, etc. etc.
The Kind numbers
cKba
guide this process.
This One-Number-Mann-Lady-Kind cascade can be pushed further with more Kinder
dcKba
and still further by a super-cascade with Jazzz numbers that iterate over this Kinder cascade.
I thought I'd stop and retire at Jazzz 5. By that time infinity is still far away, but the way ahead has been sweeped clear and perhaps our formula vehicle can be automated, so I won't have to type all this by hand.
"That'll do Pig"
This ninth episode ends the NovaLoka weblog "On the number horizon" series 1 2 3 4 5 6 7 8 9, first published as a whole at NovaLoka math.
The concept of a number horizon is a fruitful tool in understanding seemingly infinite processes. However far you count and iterate over counting numbers, infinity stays as far away as ever, but lower level numbers are lost out of sight.
In the range between one horizon and the next, numbers from a lower level build up a higher system level. As any system can be represented mathematically by a number, the good news is that above the physical level this implies divinity: a God. The bad news is there can be a cascade of systems: many higher Gods. Which one is yours?
In weblog 7
I overestimated the amount of information our universe can contain or process: a better quantum-mechanical estimate is given by the number O(4,2,4).
So if my other estimate
O(4,2,5)
is the size of a system where such a physical number still makes direct sense,
the Kingdom of Heaven should not be sought a finger further away.
It would be more intimate if some alien civilization within our own galaxy or cosmos ruled as gods, but certainly no Being nearer to infinity would bother about small fry like us.
The number gap inbetween simply doesn't allow for such involvement, any more than a man has direct knowledge about the battle between his white blood cells and bacteria.
What God worries about seeds wasted?
What man tells
Thoth what to write?
According to mathematics, this can only be a lower god, at the bottom of the cascade, one level above the material...
Either
Atum-Ra is very powerful or
Amun-Ra is high up in heaven.
And if Ra-Herakhty
seeks His association higher up, as we all like to do, then
Ra is neither Great nor Mighty:
Re is tiny, not even eternal in time,
but small fish, just like us.
I feel the iteration machinery in
weblog 8
is horrendous and unimaginable.
Likewise I do not like to apply the notion of infinity to God,
as infinity lies ever higher up the cascade...
Unless a human being has a soul that is unreachable by physical equations,
infinity is too far gone: impractical, unnecessary and cruel.
But if my soul is of a higher order than the material world, what I am doing here is totally senseless, and it would be better for me to detach myself from this world and die.
This is nothing new, it is the
Jain philosophy of 500BC.
To stay safe, because I know so little, of which I delivered mathematical proof, I must be modest. Being modest I must draw simple conclusions and do away with the qualification of God as an infinite being.
I travelled far and wide over the globe of iterations,
and it's been enough, there's no need for infinity in the real world.

"Had enough yet?"
-Ocean's 11