$* 0.2 - Indeling voor dit mathlog
freezotic als aankomend wiskundige - dag 2

Indeling
Een lezer van een weblog begint waar de schrijver (een paar uur daarvoor) is geëindigd. De communicatie verloopt discontinu en wie meer leest bladert meestal terug.
Er is ook geen stand van zaken, zoals in de wetenschap. De weblogger is voortdurend aan het breinstormen, waarbij hij de meest triviale onderwerpen niet schuwt. Als hij al een onderwerp heeft, bekijkt hij het van alle kanten.
Dit weblog zou eigenlijk over anti-geometrie moeten gaan.
Hier volgt een Legenda om het gehalte ervan weer te geven:
| Titelbalk Communicatie Symbolen | |
|---|---|
| $ | De post is klaar om ter beoordeling te laten lezen. |
| $$ | Deze post is publiceerbaar in een vaktijdschrift. |
| @ | Post vraagt erom verder te worden besproken. |
| ? | Onduidelijk is: Wat is de zin van deze post? |
| ! | Opmerkelijke post! |
| Titelbalk Kwaliteit Sterren | |
| De post is off-topic (geen ster) | |
| * | Houdt zich aan het onderwerp |
| ** | Ontwikkelt het onderwerp verder |
| *** | Bevat goede nieuwe ideeën |
| **** | Een probleem oplossende doorbraak |
| Titelbalk Onderwerp Nummering | |
| 2.1.3.0 Voorbeeld voor het losjes indelen van post | |
Na de Nederlandse post vind je onderaan een kleine Summary in het Engels.
Aparte gedeeltes kun je ook voorstellen voor Definities & Formules en voor
Links & Literatuur.
Het wijst zichzelf.
Introduced are symbols for the documentation of these weblogs, visible in the title bar:
$$ and
$ indicate the post is more or less ready for publication.
@ asks for peer council,
? is unclear and
! precedes an interesting post.
Upto 4 stars can be added to indicate a degree of penetration in the subject matter (anti-geometry).
Each weblog should be numbered to find its place in the whole of the exposition.
Sections for definitions and formulas, links and literature are added as appropriate.
Each post ends with a summary in English.
freezotic
posted on Thursday, October 25, 2007 6:37 PM


 verschijnt.
verschijnt.
 dan zou je kunnen meten dat rood 5 seconden duurt, groen 1 sec. en blauw 3 sec.
Daardoor is rood + groen = 6 sec. en elk element uit de power set van schermkleuren uniek bepaald door tijdsduur.
dan zou je kunnen meten dat rood 5 seconden duurt, groen 1 sec. en blauw 3 sec.
Daardoor is rood + groen = 6 sec. en elk element uit de power set van schermkleuren uniek bepaald door tijdsduur.



 }
} en je krijgt oneindig veel meer!
en je krijgt oneindig veel meer!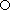 nul-punt.
nul-punt.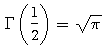 tot onze verbazing van het getal -1/2 de faculteit !
tot onze verbazing van het getal -1/2 de faculteit !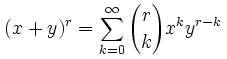

Feedback
# re: $*** 1.1.1 - Gedachten over afstand 5/19/2005 11:59 PM philip
Hé hier word ik weer helemaal wakker van.
Lang geleden dat ik aan combinaties en permutaties geroken heb.
Leuk om dit te lezen.
En chapeau voor de mooie vormgeving van je weblog!
# re: $*** 1.1.1 - Gedachten over afstand 5/20/2005 5:37 PM freeZotic
Dank je wel!
Een Permutatie Pk is een ordening van een k aantal elementen.
Bijvoorbeeld: abc, dan zijn de permutaties: abc, acb, bac, bca, cab, cba
Vergelijking voor permutatie met dubbelen: k!/a!/b!/c!... (a is aantal keren a, etc.)
Permutatie zonder dubbelen is dus: k!
Een Variatie rVk is een keuze van k elementen uit een set van r, waarbij de volgorde van de elementen er wel toe doet.
Vergelijking voor variatie: n!/(n-k)!
Bij een combinatie rCk doet de volgorde er niet toe. Dus dan wordt de vergelijking: rCk = rVk / Pk = n!/(n-k)!/k!
F!